1289. Minimum Falling Path Sum II  ¶
¶


Problem
Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.
A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.
Example 1:
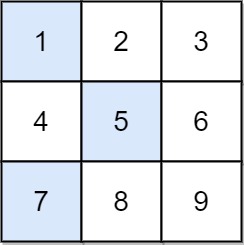
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: 13 Explanation: The possible falling paths are: [1,5,9], [1,5,7], [1,6,7], [1,6,8], [2,4,8], [2,4,9], [2,6,7], [2,6,8], [3,4,8], [3,4,9], [3,5,7], [3,5,9] The falling path with the smallest sum is [1,5,7], so the answer is 13.
Example 2:
Input: grid = [[7]] Output: 7
Constraints:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99

