1462. Course Schedule IV ¶

Problem

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [a_i, b_i] indicates that you must take course a_i first if you want to take course b_i.

For example, the pair [0, 1] indicates that you have to take course 0 before you can take course 1.

Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.

You are also given an array queries where queries[j] = [u_j, v_j]. For the j^th query, you should answer whether course u_j is a prerequisite of course v_j or not.

Return a boolean array answer, where answer[j] is the answer to the j^th query.

Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0.
Course 0 is not a prerequisite of course 1, but the opposite is true.

Example 2:

Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites, and each course is independent.

Example 3:

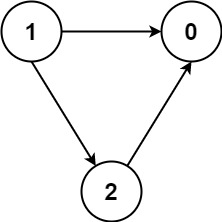
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

Constraints:

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
All the pairs [a_i, b_i] are unique.
The prerequisites graph has no cycles.
1 <= queries.length <= 10⁴
0 <= u_i, v_i <= n - 1
u_i != v_i