1536. Minimum Swaps to Arrange a Binary Grid ¶

Problem

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

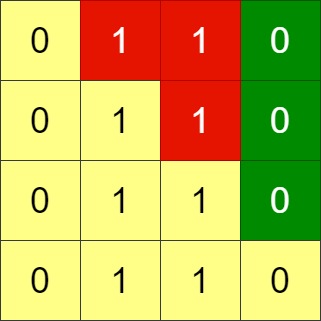
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

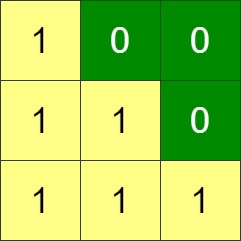
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

Constraints: