2002. Maximum Product of the Length of Two Palindromic Subsequences  ¶
¶



Problem
Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.
Return the maximum possible product of the lengths of the two palindromic subsequences.
A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.
Example 1:
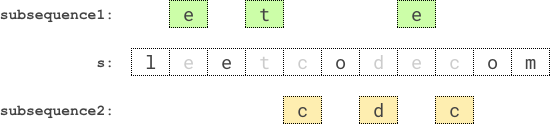
Input: s = "leetcodecom" Output: 9 Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence. The product of their lengths is: 3 * 3 = 9.
Example 2:
Input: s = "bb" Output: 1 Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence. The product of their lengths is: 1 * 1 = 1.
Example 3:
Input: s = "accbcaxxcxx" Output: 25 Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence. The product of their lengths is: 5 * 5 = 25.
Constraints:
2 <= s.length <= 12sconsists of lowercase English letters only.

