2033. Minimum Operations to Make a Uni-Value Grid ¶

Problem

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

Example 1:

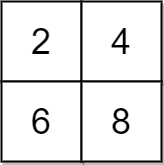
Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

Example 2:

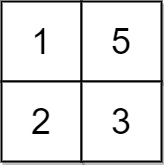
Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

Example 3:

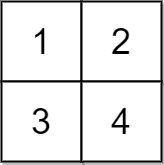
Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
1 <= x, grid[i][j] <= 10⁴