2087. Minimum Cost Homecoming of a Robot in a Grid  ¶
¶


Problem
There is an m x n grid, where (0, 0) is the top-left cell and (m - 1, n - 1) is the bottom-right cell. You are given an integer array startPos where startPos = [startrow, startcol] indicates that initially, a robot is at the cell (startrow, startcol). You are also given an integer array homePos where homePos = [homerow, homecol] indicates that its home is at the cell (homerow, homecol).
The robot needs to go to its home. It can move one cell in four directions: left, right, up, or down, and it can not move outside the boundary. Every move incurs some cost. You are further given two 0-indexed integer arrays: rowCosts of length m and colCosts of length n.
- If the robot moves up or down into a cell whose row is
r, then this move costsrowCosts[r]. - If the robot moves left or right into a cell whose column is
c, then this move costscolCosts[c].
Return the minimum total cost for this robot to return home.
Example 1:
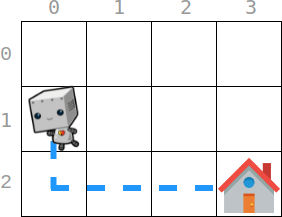
Input: startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7] Output: 18 Explanation: One optimal path is that: Starting from (1, 0) -> It goes down to (2, 0). This move costs rowCosts[2] = 3. -> It goes right to (2, 1). This move costs colCosts[1] = 2. -> It goes right to (2, 2). This move costs colCosts[2] = 6. -> It goes right to (2, 3). This move costs colCosts[3] = 7. The total cost is 3 + 2 + 6 + 7 = 18
Example 2:
Input: startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26] Output: 0 Explanation: The robot is already at its home. Since no moves occur, the total cost is 0.
Constraints:
m == rowCosts.lengthn == colCosts.length1 <= m, n <= 1050 <= rowCosts[r], colCosts[c] <= 104startPos.length == 2homePos.length == 20 <= startrow, homerow < m0 <= startcol, homecol < n

